首页 集算器 函数参考 Function lineplan () 前一篇 | 后一篇

lineplan ()

阅读（1946） 标签: 线性规划, 约束条件, 极值,

描述：

线性规划，求解线性约束条件下线性目标函数极值问题。

语法：

lineplan(A,B,C)

备注：

本函数使用单纯形法，除可解决常规的线性规划问题外，还可解决基本解不是可行解的情况。获取参数时需将问题转换为如下标准型：

 

目标函数：

线性不等式约束：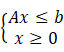

备注：

外部库函数，外部库的使用请参考《外部库使用指南》。

线性规划，求解线性约束条件下线性目标函数极值问题。

注意结果的选取：输出极值和极值点坐标，极值为第一个子序列的第一个数值乘以-1，极值点坐标为第二个子序列中前n个数值，n为x数量。

参数：

A

序列，系数矩阵。

B

序列，约束矩阵。

C

目标函数矩阵。

返回值：

序列

示例：

Ø  求解由线性不等式定义的简单线性规划

常规算例：

 

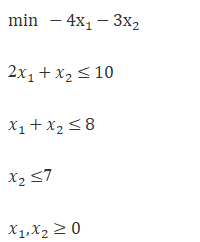
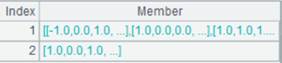
A

 

1

[[2,1],[1,1],[0,1]]

输入系数矩阵A。

2

[[10,0],[8,0],[7,0]]

输入约束矩阵B。

3

[[-4,-3],[0,0],[0,0]]

输入目标函数矩阵C。

4

=lineplan(A1,A2,A3)

取结果：目标函数极小值为-26，极值坐标（2.0,6.0）。

 

特殊算例：

 

A

 

1

[[1,1],[-1,-1]]

输入系数矩阵A。

2

[[2,0],[-1,0]]

输入约束矩阵B。

3

[[1,2],[0,0]]

输入目标函数矩阵C。

4

=lineplan(A1,A2,A3)

取结果：目标函数极小值为1，极值坐标（1.0,0.0）。