Math
1. MathCli外部库文件路径为:[安装目录]\ esProc\extlib\ MathCli;润乾外部库核心jar为scu-math-cli-2.10.jar。
ejml-core-0.40.jar
ejml-ddense-0.40.jar
ejml-simple-0.40.jar
libsvm-3.25.jar
注:以上第三方依赖jar,外部库压缩包中默认已放置,用户可根据实际应用环境灵活使用。
2. 访问math外部库可使用的外部库函数有chi2inv()、cov()、covm()、dism()等。函数用法请参考【帮助】-【函数参考】。
3. MathCli外部库提供一些线性代数相关函数,下面列举常见用法:
(1)生成矩阵
在MathCli中,可以用一些函数生成0矩阵、单位矩阵等,如:
|
|
A |
B |
|
1 |
=I(3) |
|
|
2 |
=eye(3) |
=eye(4, 3) |
|
3 |
=ones(3) |
=ones(4, 3) |
|
4 |
=zeros(3) |
=zeros(4, 3) |
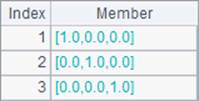
使用I()函数和eye()函数都可以生成单位矩阵,单位矩阵是指主对角线为1,其它位置为0的矩阵,不同之处在于I()函数只能用来定义方阵。A1、A2和B2中结果如下:


与eye()函数有些类似,ones()和zeros()可以用来生成1矩阵和0矩阵,与eye()不同的是这两个函数还可以增加参数定义多维矩阵。A3~B4中的结果如下:




(2)多维矩阵运算
使用mfind(A, n)函数,可以在向量或矩阵A中查找前n个非0成员的位置,如:
|
|
A |
B |
|
1 |
[0,,3,2,0,2,1,0] |
=mfind(A1) |
|
2 |
=mfind(A1,3) |
=mfind(A1,10) |
|
3 |
[[1,0,2],[0,0,2],[0,4,7]] |
=mfind(A3) |
|
4 |
=mfind(A3,3) |
=mfind(A3,10) |
在向量中查找时,返回的结果是非0成员在向量中的序号构成的数列,位置从1开始。不设置n时,只返回第1个非0非空成员的位置,B1结果如下:

通过设置n,可以返回前n个非零成员的位置,如果所有非0成员的个数小于n,则返回所有非0非空成员的位置。A2和B2中结果如下:


在矩阵中查找时,返回的结果是非0成员在矩阵中的序号构成的数列,从第1列开始依次计算,如3行的矩阵中,第1列位置分别为1,2,3,第2列位置分别为4,5,6,以此类推。不设置n时,只返回第1个非0非空成员的位置,B3结果如下:

通过设置n,可以返回前n个非零成员的位置,如果所有非0成员的个数小于n,则返回所有非0非空成员的位置。A4和B4中结果如下:


在外部库MathCli中,可以用msum(A, n) 函数在矩阵或多维矩阵中汇总求和,其中为汇总的维度层数,如:
|
|
A |
B |
|
1 |
[[11,12,13],[21,22,23],[31,32,33]] |
=msum@a(A1) |
|
2 |
=msum(A1, 1) |
=msum(A1, 2) |
|
3 |
[[[111,112,113],[121,122,123],[131,132,133]],[[211,212,213],[221,222,223],[231,232,233]]] |
=msum@a(A3) |
|
4 |
=msum(A3, 1) |
=msum(A3, 2) |
A1中定义了普通矩阵如下:

使用@a选项时,msum函数会计算矩阵中所有成员的和,B1中结果如下:

通过设置n,可以指定汇总层数,不设置相当于对第1层汇总,如果第1层只有单一成员,则对第2层汇总,以此类推。对矩阵而言对第1层汇总即各行相加求和,对第2层汇总即各列相加求和。A2和B2中结果如下:


A3中定义了3维矩阵如下,它的2个成员都是3*3矩阵:

使用@a选项时,msum函数同样会计算多维矩阵中所有成员的和,B3中结果如下:

通过设置n,可以指定汇总层数,不设置相当于对第1层汇总。对多维矩阵而言对第1层汇总即上面两个矩阵对位相加求和,对第2层汇总即上面两个矩阵中分别计算每列成员的和。A4和B4中结果如下:


在外部库MathCli中,还可以用mcumsum(A, n) 函数在矩阵或多维矩阵中计算累积求和,如:
|
|
A |
B |
|
1 |
[[11,12,13],[21,22,23],[31,32,33]] |
=mcumsum(A1) |
|
2 |
=mcumsum(A1, 2) |
=mcumsum@z(A1) |
|
3 |
[[[111,112,113],[121,122,123],[131,132,133]],[[211,212,213],[221,222,223],[231,232,233]]] |
|
|
4 |
=mcumsum(A3) |
=mcumsum(A3, 2) |
使用mcumsum函数得到的是累积求和,与普通求和不同,B1和A2中分别计算矩阵各行累积和各列累积的结果,如下:


在矩阵中计算累积求和时,可以添加@z选项,逆向累积。B2中结果如下:

在多维矩阵中计算累积求和时,同样可以指定汇总层数,不设置相当于对第1层执行累积求和。A4和B4中结果如下:


使用mmean(A, n) 函数在矩阵或多维矩阵中计算均值,如:
|
|
A |
B |
|
1 |
[[11,12,13],[21,22,23],[31,32,33]] |
=mmean@a(A1) |
|
2 |
=mmean(A1) |
=mmean(A1, 2) |
|
3 |
[[[111,112,113],[121,122,123],[131,132,133]],[[211,212,213],[221,222,223],[231,232,233]]] |
=mmean@a(A3) |
|
4 |
=mmean(A3) |
=mmean(A3, 2) |
与求和类似,使用@a选项时,mmean函数会计算矩阵中所有成员的均值,B1中结果如下:

与求和类似,mmean函数也可以指定汇总层数,A2和B2中分别计算矩阵各列均值与各行均值,结果如下:


在多维矩阵中计算均值时,同样可以使用@a选项计算所有成员的均值,B3中结果如下:

在多维矩阵中计算均值时,也可以指定汇总层数。A4和B4中结果如下:


在MathCli中,还可以使用mtd(A, n) 函数在矩阵或多维矩阵中计算标准差,如:
|
|
A |
B |
|
1 |
[[11,12,13],[21,22,23],[31,32,33]] |
=mstd(A1) |
|
2 |
=mstd(A1, 2) |
=mstd@s(A1) |
|
3 |
[[[111,112,113],[121,122,123],[131,132,133]],[[211,212,213],[221,222,223],[231,232,233]]] |
=mstd(A3) |
|
4 |
=mstd(A3, 2) |
=mstd@s(A3) |
与求和类似,mstd可以指定汇总层数,计算标准差,B1和A2中分别计算矩阵各列标准差与各行标准差,结果如下:


计算标准差时,可以使用@s选项使用统计算法,求均值时用n-1计算,B2中结果如下:

在多维矩阵计算标准差与求和类似, B3和A4中结果如下:


B4中添加了@s选项,计算结果如下:

使用mnorm(A, n) 函数,可以指定维度,将矩阵或多维矩阵中的数据做归一化处理,使得指定汇总层数的均值为0,标准差为1。如:
|
|
A |
B |
|
1 |
[[11,12,13],[21,22,23],[31,32,33]] |
=mnorm(A1) |
|
2 |
=mnorm(A1, 2) |
=mnorm@s(A1) |
|
3 |
[[[111,112,113],[121,122,123],[131,132,133]],[[211,212,213],[221,222,223],[231,232,233]]] |
=mnorm(A3) |
|
4 |
=mnorm(A3, 2) |
=mnorm@s(A3) |
函数mnorm的使用与前面几个函数都类似,B1和A2中分别将矩阵各列与各行的数据归一化处理,结果如下:


使用@s选项时,归一化处理的标准差计算使用统计学算法,B2中结果如下:

在多维矩阵计算标准差与求和类似, B3和A4中结果如下:


B4中添加了@s选项,计算结果如下:

(3)逆累积分布函数
在MathCli中,提供了一些逆累积分布函数,如:
|
|
A |
|
1 |
=norminv(0.25, 2, 1) |
|
2 |
=tinv(0.99, 2) |
|
3 |
=finv(0.95,5,10) |
|
4 |
=chi2inv(0.95,10) |
函数norminv(p, mu, sigma)用来计算正态逆累积分布,概率p在(0, 1)在区间内,mu为设定的均值,sigma为设定的标准偏差值,A1中结果如下:

函数tinv(p, nu)用来计算T逆累积分布,概率p在(0, 1)区间内,nu为概率对应的自由度,A2中结果如下:

函数finv(p, v1, v2)用来计算F逆累积分布,概率p在(0, 1)区间内,v1为分子自由度,v2为分母自由度,A3中结果如下:

函数chi2inv(p, v)用来计算卡方逆累积分布,概率p在(0, 1)区间内,v自由度,A4中结果如下:

