运算模型
基本概念：
集合
一些确定的事物汇集成为集合，构成集合的事物称为集合的元素或者成员。在润乾报表中，集合的元素一般是数据、单元格、行、列、记录、字段、组等。
数组
将有限集的元素按照某种规则排序，得到一个有先后次序的序列，称为数组。数组的成员个数称为数组的长度。数组是集合的一种特殊情况。
集合函数和操作符
运算结果为集合的函数，我们称为集合函数；运算结果为集合的操作符，我们称为集合操作符。
集合函数有select()、group()、list()、query()、call()、to()等。
集合表达式和单值表达式
计算结果为集合的表达式称为集合表达式。
计算结果为单值的表达式称为单值表达式。
扩展模型
扩展单元格
当单元格的数据值表达式为集合表达式时，该单元格默认为可扩展单元格。可以为扩展单元格设置一个扩展方向，扩展可以有横纵两个方向，即横向扩展和纵向扩展，但一个扩展格同时只能有一个扩展方向。
横向扩展
描述
l 当可扩展单元格的扩展方向为横向时，该单元格进行的扩展称为横向扩展。此时该单元格会横向进行复制，复制出的单元格的数据值依次为表达式的结果数据值，表达式返回几个值，单元格就复制几个。
l 复制出来的新单元格的所有属性都引用被复制单元格的属性；
图例
纵向扩展
描述
l 当可扩展单元格的扩展方向为纵向时，该单元格进行的扩展称为纵向扩展。此时该单元格会纵向进行复制，复制出的单元格的数据值依次为表达式的结果数据值，表达式返回几个值，单元格就复制几个。
l 复制出来的新单元格的所有属性都引用被复制单元格的属性；
图例
不可扩展
当单元格的数据值表达式为单值表达式时，该单元格默认为不可扩展单元格。
主格模型
基本概念
报表左上角的灰色单元格称为报表首格，也称为根格。它用于存储描述整个报表的属性，同时他在层次坐标中有特殊的意义。层次坐标会在后面的章节中介绍。如下图所示：
根格（报表首格）的书写规则为：`0
这里要强调的是 `0而不是‘0
主格和附属格
单元格进行扩展的过程中，缺省情况下，相对于其右（下）边的单元格而言，扩展格是主动复制的，被称为其它格（其右/下的格）的主格，而其右（下）的单元格是被动跟随复制的，被称为扩展格的附属格或子格。主格和附属格是相对的概念，即某格是另一格的主格或附属格，不存在单独的主格和附属格。
从主格的定义中看，显然只有扩展格才能是其它格的主格！
要注意的是，在缺省情况下，扩展格左（上）的格并不是其附属格，只有右（下）的格才是其附属格。
特别地，某个单元格的主格属性可以人为被改变。
左主格和上主格
单元格进行纵向扩展时，我们又称其为其它格（其右/下的格）的左主格，而横向扩展时则称为上主格。一个单元格可以既有左主格又有上主格。
特别地，某个单元格的左主格或者上主格属性可以人为的被改变，即可以人为的把某个纵向扩展格右边的单元格设为他的左主格，或者把某个横向扩展格下方的单元格设为他的上主格。
多层扩展
多个单元格同时进行扩展时，一个扩展格可以既是某些格的主格又是另一个扩展格的附属格，这种情况下就形成多层扩展的情况。如果主格A1的附属格是B1，而B1还有附属格C1，那么B1称为A1的1级子格（或1级附属格），C1称为A1的2级子格（或2级附属格），同时A1称作B1的1级主格，A1称作C1的2级主格。如果C1再有附属格D1，那么A1是D1的3级主格，而D1是A1的3级子格。显然，B1是D1的2级主格，D1是B1的2级子格。
l 同一行（列）上有两个或更多的扩展格。左（上）边的扩展格将是右（下）边的扩展格的主格，右（下）边的扩展格是其左（上）边扩展格的附属格，同时又是其右（下）边单元格的主格。
图示：
直接主格和直接附属格
单元格进行多层扩展时，若主格A的附属格B不再有任何同方向的主格是该主格A的附属格，则称B为A在该方向上的直接附属格，也称为一级附属格；反之，A称为B的直接主格，也称为一级主格。
规则
缺省主格认定
单元格横向扩展时，上方横向扩展单元格缺省为它的上主格，下方单元格缺省为它的附属格；如果上方没有横向扩展格，则上主格缺省为 `0 格
单元格纵向扩展时，左边纵向扩展单元格缺省为它的左主格，右边单元格缺省为它的附属格；如果左边没有纵向扩展格，则左主格缺省为 `0 格
人为改变主格规则
除了的前面提到的缺省情况外，我们允许人为地改变单元格的主格。可以将某个单元格的左主格设置成某个纵向扩展格、上主格设置的某个横向扩展格，左主格和上主格是分别设置的。
为了符合扩展变化的规则，我们可以知道人为设置主格需要满足一些条件：
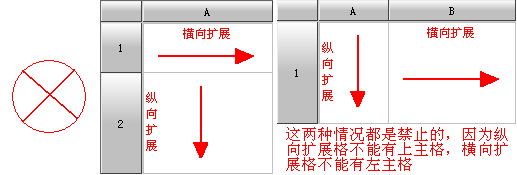
Ø 左主格必须是纵向扩展格，上主格必须是横向扩展格，否则设置无效。
Ø 不允许出现循环设置的情况，即设置A的主格是B，B的主格是C，C的主格又是A，出现循环设置时认为设置有误，报表无法计算。显然，在缺省的情况下是不可能出现循环设置的，而在人为设置时必须避免这种情况的出现。
Ø 横向扩展格不允许有左主格，纵向扩展格不允许有上主格。
人为设置时，可能发生左（上）主格在右（下）边的情况，而且主格也不一定和附属格在同一行（列）上。
例1：
扩展变化规则
多层扩展时，扩展次序是从主到次的，即先扩展主格，然后扩展其附属格，再扩展其二级附属格，依此类推。
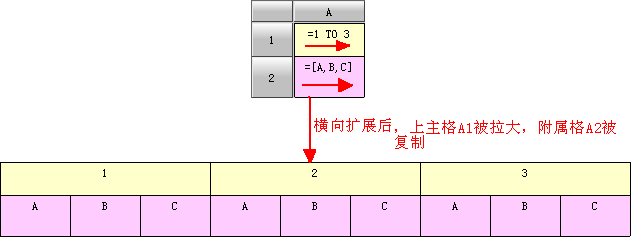
单元格进行横向扩展时，会将其同列的上主格拉大，把其附属单元格复制，特别地，如果其某个上主格不在同列上，则该上主格不会被拉大；
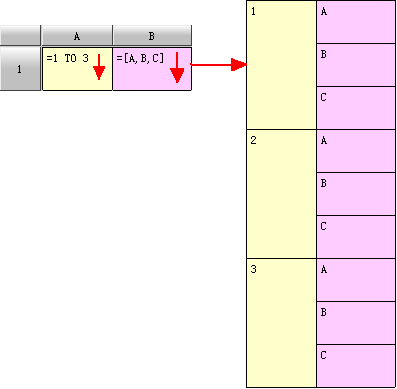
单元格进行纵向扩展时，会将其同行的左主格拉大，把其附属单元格复制，特别地，如果其某个左主格不在同行上，则该左主格不会被拉大。
一般地，主格能够主动进行扩展复制，称为主动扩展格；附属单元格被主单元格带动着复制，称为被动复制格。由于附属单元格同时又可能是别的单元格的主格，本身还可以进行主动扩展复制，因此主动扩展格和被动复制格是相对的。既不能主动扩展复制，也不能被动复制的单元格，我们称为不可复制格，或者叫固定格。
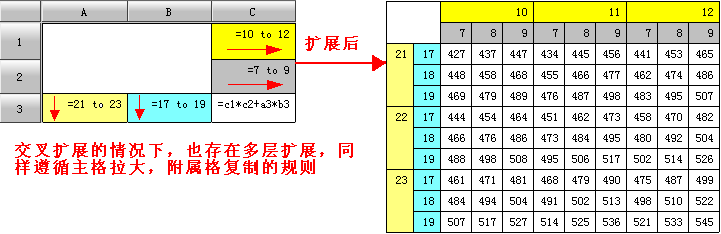
同一报表中可能同时有纵向扩展格和横向扩展格，如果它们的子格有重叠部分，则这些子格就即有左主格又有上主格，在扩展时会被即向下又向右复制，形成一片矩形单元格区域，从而做到交叉扩展。相应地，在这种机制下，多层交叉也不难实现。
在交叉扩展中，有的单元格有可能既被横向扩展向右复制，也被纵向扩展向下复制，可是，单元格的横向扩展与纵向扩展这两种扩展是相互独立的，既可以先进行横向扩展，也可以先进性纵向扩展，并不会影响扩展之后的结果。
例2：
例3：
例4：
例5：
缺省情况下，在单元格中的运算中可以引用其它单元格的值，直接写单元格名即可，这样的运算称为格间运算，这种引用称为缺省的引用规则。在这里，被引用的单元格必须是能够由当前格唯一确定的。
一般情况下，被引用单元格往往是当前格的主格，或者与当前格有相同的一级主格，或者是固定格。固定格由于不能复制，因此可以唯一确定。
例1：
扩展前：
|
商品号 |
库存量 |
|
A2 |
B2 |
扩展后：
|
商品号 |
库存量 |
|
001 |
23 |
|
005 |
14 |
|
121 |
69 |
|
134 |
22 |
其中B2单元格的表达式： ds2.sum(stock, product_id==A2)
可以看到，B2单元格引用了A2单元格，因为A2是B2的主格，因此B2可以引用A2。
例2：
从图中可以看出，C1单元格引用了B1单元格的值，这里，B1的一级主格是A1，C1的一级主格是A1，因此B1和C1有共同的一级主格，因此C1可以引用B1。
例3：
从图中可以看出，B2单元格的表达式引用了A1单元格，A1单元格是个固定格，既不可以主动扩展复制也不可以被动复制，因此B2可以引用A1。
层次坐标
层次坐标
在进行报表设计时，单元格尚未进行扩展，但是其它某些单元格的表达式往往需要对这个单元格扩展后的单元格进行精确定位并运算。
例1：
|
月份 |
产值 |
|
A2(月份) |
B2 |
|
其中 三月份产值为： |
B3 |
扩展后：
|
月份 |
产值 |
|
1月 |
|
|
2月 |
|
|
3月 |
|
|
4月 |
|
|
5月 |
|
|
6月 |
|
|
7月 |
|
|
8月 |
|
|
其中 三月份产值为： |
需要定位到3月份对应的产值并返回 |
对单元格B3来说，需要从B2扩展出来的单元格中找到对应月份为3月的格子然后返回其值。
然而B2能扩展出几个格子以及每个格子在什么位置，在扩展前很难描述，因此，为了避免混淆，应该对扩展后的每个单元格进行唯一性定义，这就是单元格的层次坐标。层次坐标是用于唯一描述（精确定位）扩展后的每一个单元格的表达式。
层次坐标的运算结果返回目标单元格。如果层次坐标能够定位到一个单元格，那么返回该单元格的值，如果定位到多个单元格，那么返回这些单元格中的第一个单元格的值。
表达式规则：
说明：
(a)
为Cellx的左主格，
为左主格扩展后的次序，即扩展后的第几个单元格，如果不指定或者为0，则表示为当前表达式所在单元格所属的当前左主格，Cellx为目标单元格，应该为
，
…
的附属单元格。与之类似，Tk为Cellx的上主格，tk为上主格扩展后的次序。
(b) 如果只有上主格，没有左主格，分号不能省略，即应该写成：
Cellx [；Tk：tk, Tk-1： tk-1,……T1： t1]
如果只有左主格，没有上主格，分号可以省略，即可以写成：
Cellx [Lk：lk, Lk-1：lk-1,……L1：l1 ]
(c)
与Tk的次序是从远到近的，也就是说越上级的主格越靠前。而找到层次坐标所表示单元格的次序是从最上级的主格开始。
如：
C1[A1:2,B1:1]找C1的次序是：先找单元格A1展开后的第2格，再找第二个A1下属的B1单元格扩展出来的第一个B1，然后找到和该B1对应的C1。
(d) 完整的层次坐标表达式应该包括Cellx的所有主格，层次坐标与写在哪个单元格中无关。
例2：
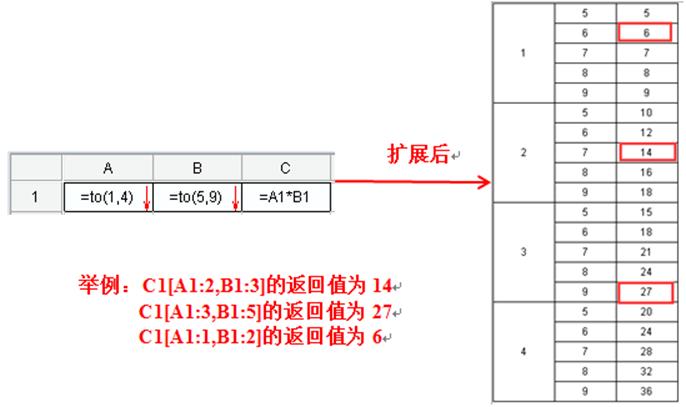
例3：
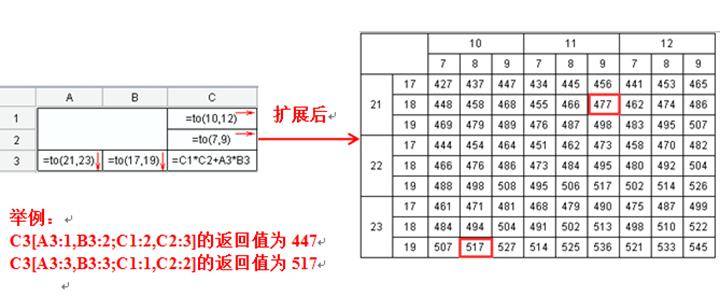
位移坐标
有了层次坐标后，很多时候并不够用，因为大部分时候报表设计者并不知道目标单元格的具体位置，仅仅知道目标单元格相对于当前单元格的位置，基于这种考虑，我们给出了位移坐标，从而层次坐标更多时候成了模型上的意义，而非应用上的意义。
位移坐标的运用非常广泛，例如报表中常常需要计算同期比、比上期之类的与时间相关的运算，而这些运算往往需要用到下一行的数据减上一行数据，后一列数据减前一列数据，等等，这种涉及到相邻n行或者n列的行间、列间的运算，称为位移运算，相关的表达式称为位移表达式。
位移坐标是用来描述目标单元格和当前格之间的位置关系的表达式。
表达式规则：
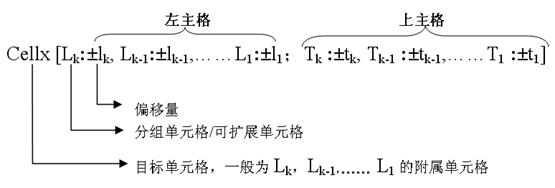
说明：
1、 Lk为Cellx的左主格，lk为单元格的偏移量，即当前格所属的Lk主格和目标格所属的Lk主格之间的偏移量，如果不指定lk，则表示为当前所在的左主格Lk，Cellx为目标单元格，一般为Lk，Lk-1，。。。。。。L1的附属单元格
2、 如果没有左主格，只有上主格的话，分号不能省略，即写成Cellx [；Tk ：±tk, Tk-1 ：±tk-1,……T1 ：±t1]
3、 如果没有上主格，只有左主格的话，分号可以省略，即写成Cellx [Lk：±lk, Lk-1：±lk-1,……L1：±l1 ]
4、 Lk的次序是从远到近的，也就是从离当前格最远的主格开始的，也可以理解为从最高级别的主单元格开始
5、 完整的位移坐标表达式应该包括Cellx的所有主格，位移坐标与写在哪个单元格中紧密相关。
例1：
坐标缺省表示法
由于层次坐标和位移坐标的表示很烦琐，而大部分时候对于单元格的定位是和当前格的位置有关系的，一般是指当前格的主格或者和当前格有着相同主格的单元格，此时可以采用缺省的写法。
缺省情况下，如果目标单元格的某个主格Lk和当前单元格的主格相同，那么层次坐标(位移坐标)中该主格可以不写
如果目标单元格与当前格的关系满足缺省引用规则，那么直接遵循该规则的引用表示法，不需要层次坐标(位移坐标)。
例1：
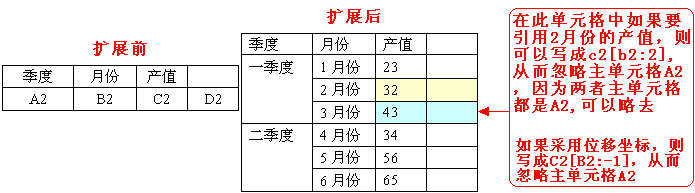
根坐标表示法
描述：
在前面我们提到了根格的概念，即报表有个首格（根格），报表中的扩展单元格是逐级扩展的，有主格、附属格的概念，呈树状的结构，而根格则是这棵树的根。如下图所示：
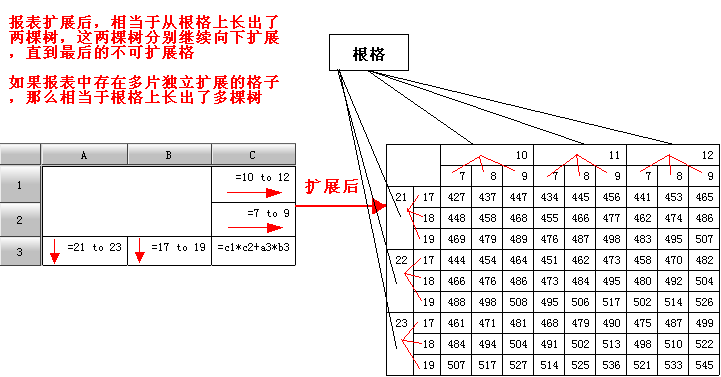
由此可以看出，单元格逐级扩展后实际形成了以根格（报表首格）为根的一棵树，报表中存在多片独立扩展，那么根上就长出多棵树，每一个可主动扩展的格子都是树上的一个节点，最末一级的不可扩展格则是节点上的叶子。而层次坐标相当于描述任意一个节点或者叶子到达根的路径。
由于根格是客观存在的，而树上的所有节点都是由根格发展而来，因此前面介绍的层次坐标忽略了根节点的描述，下面我们加上根坐标的描述，把层次坐标重新表示一下：
表达式规则：
cellx[`0, Lk:lk, Lk-1:lk-1,……L1:lk; `0, Tk:tk, Tk-1:tk-1,……T1:t1]
从上面的层次坐标可以看出，完整的层次坐标是从根上开始的，而`0 则代表根坐标。
&运算符
描述：
从前面的介绍可知，单元格是可以扩展的，一个格子可以扩展出多个，那么如何知道某个扩展出来的格子在所有扩展出来的格子中排第几呢？此时我们就引入了&运算符，他可以获得当前格所属的某主格在所有扩展出来的格子中排第几，这种运算我们也称为层次坐标的逆运算。
表达式规则：
&cellx
返回值：
整数，当前格所属的cellx主格在所有扩展出来的格子中的排序
说明：
cellx必须是当前格的主格，这样&cellx才能够正确运算，其返回值相当于是当前格所属的cellx主格的位置
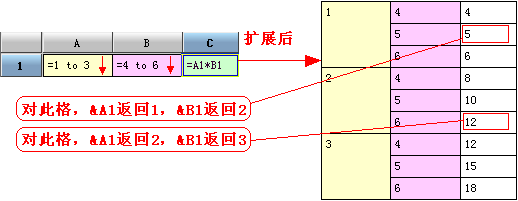
格集
在实际应用中，往往需要对一组单元格进行运算，而不是单个单元格。这些单元格有可能是固定格，也有可能是主动扩展、被动复制格，为了能在表达式中描述确定的一组单元格，我们引入格集的概念。
格集
格集可以看为满足某种条件的一组单元格的集合。特别的，单个单元格也可以视为仅含一个单元格的格集。
为了说明格集的概念及其作用，我们看看下面的表格：
例1：
扩展前：
|
A1 |
B1 |
C1 |
D1 |
|
A2 |
B2 |
C2 |
D2 |
扩展后：
|
a1 |
b1 |
c1 |
d1 |
|
a2 |
b2 |
c2 |
d2 |
|
c3 |
d3 |
||
|
b4 |
c4 |
d4 |
|
|
c5 |
d5 |
||
|
a6 |
b6 |
c6 |
d6 |
|
c7 |
d7 |
||
|
c8 |
d8 |
||
|
b9 |
c9 |
d9 |
|
|
c10 |
d10 |
||
|
b11 |
c11 |
d11 |
|
|
c12 |
d12 |
填入数据：
|
客户 |
产品 |
日期 |
金额 |
|
Tom |
牛奶 |
2005-5-1 |
12.00 |
|
2005-5-12 |
20.00 |
||
|
毯子 |
2005-2-21 |
2.00 |
|
|
2005-3-1 |
1.00 |
||
|
Jerry |
牛奶 |
2005-1-1 |
12.00 |
|
2005-1-12 |
100.00 |
||
|
2005-5-1 |
24.00 |
||
|
饼干 |
2005-2-1 |
3.00 |
|
|
2005-5-13 |
4.00 |
||
|
奶酪 |
2005-2-1 |
6.00 |
|
|
2005-4-1 |
2.00 |
如果我们要进行如下统计：①Tom买牛奶的日期；②Tom买毯子的金额；③Jerry在2005-2-1买的商品；④所有买牛奶的金额。
在做这些统计时，涉及到的数据都是发生在一系列格子中的，我们分别来看一下：①c2,c3；②d4,d5；③d9,d11；④d2,d3,d6,d7,d8。
格集表示法
固定格的格集表示法
对于固定的单元格，我们可以用list()函数，：（link）操作符来表示，书写规则如下：
list(Cell1, Cell2, Cell3,……Celln) 表示由Cell1, Cell2, Cell3,……Celln组成的格子的集合
[Cellx : Celly] 其中Cellx与Celly均为单元格，该表达式表示以Cellx与Celly为对角点圈起的矩形区域，而且，Cellx在左上角，Celly在右下角。
提示：Link操作符返回的结果是一个格集，可以对其应用集合函数，如count()、sum()、max()、min()等，但是包含link操作符的单元格不允许设为扩展格。
举例：
list(A1,B3,C4) 表示由A1,B3,C4三个单元格组成的集合
sum([A1:B3]) 表示对以A1与B3为对角点圈起的矩形区域里的格子求和。
扩展格的格集表示法
对于扩展格的格集表示，我们一般和层次坐标结合起来，由层次坐标来界定一个范围，在这个范围内的所有单元格的集合，其书写规则如下：
cellx[层次坐标或者位移坐标]{}
说明：从上述书写规则可以看出，格集相当于在层次坐标或者位移坐标的基础上增加了{}，即可表示该层次坐标或者位移坐标界定的范围内的所有单元格。前文已经提到，如果没有{}，而层次坐标界定的范围内的单元格不止一个，那么该层次坐标返回的是该范围内的第一个单元格，有了{}，就返回该范围内单元格的集合。
例1：
扩展前：
|
A1 |
B1 |
C1 |
D1 |
|
A2 |
B2 |
C2 |
D2 |
扩展后：
|
a1 |
b1 |
c1 |
d1 |
|
a2 |
b2 |
c2 |
d2 |
|
c3 |
d3 |
||
|
b4 |
c4 |
d4 |
|
|
c5 |
d5 |
||
|
c6 |
d6 |
||
|
a7 |
b7 |
c7 |
d7 |
|
c8 |
d8 |
||
|
c9 |
d9 |
||
|
b10 |
c10 |
d10 |
|
|
c11 |
d11 |
||
|
c12 |
d12 |
根据上述表格，我们写几个格集并分析其结果由哪些单元格组成。
C2[`0]{} 返回扩展后的c2,c3,c4,c5,c6,c7,c8,c9,c10,c11,c12
C2[A2:2]{} 返回扩展后的c7,c8,c9,c10,c11,c12
D2[A2:1,B2:2]{} 返回扩展后的d4,d5,d6
缺省格集
同样的，为了简化格集的表示，很多时候会有缺省的写法，其缺省的规则和层次坐标、位移坐标完全一样，主要也是为了简化其中的层次坐标、位移坐标的写法，即目标单元格和当前格的主格相同时，层次坐标（位移坐标）中的该主格可以省略，如果所有主格都相同，则层次坐标（位移坐标）可以为空，甚至连中括号都可以省略。
其书写规则为：
cellx[缺省的层次坐标或者位移坐标]{}
如果层次坐标（位移坐标）完全省略，则缺省的写法为：
cellx[]{}或Cellx{}
例1：
例2：
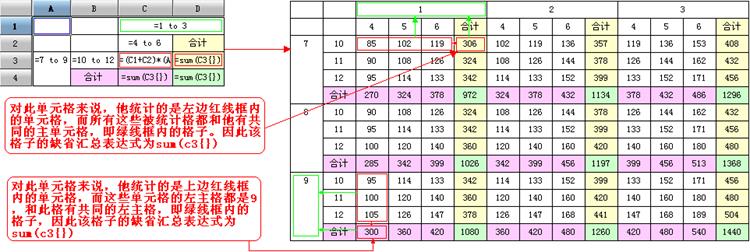
格集的条件表达式
如前文所述，当需要对一组单元格进行操作时，我们引入了格集表示法，但是格集的表示是和层次坐标、位移坐标紧密相关的，即层次坐标或者位移坐标确定的范围内的单元格的集合，缺省情况下则是当前格所属的主格管辖范围内所有目标单元格的集合。
但是，很多时候，我们需要运算的目标不是层次坐标确定的所有单元格集合，而是该范围内满足某种条件的单元格集合，此时我们引入了条件表达式，其书写规则如下：
cellx[层次坐标或者位移坐标]{条件表达式}
从上面的表达式可以看出，其含义是对层次坐标或者位移坐标界定的单元格集合再运用条件表达式进行过滤，把符合条件的单元格找出来，并返回。
例1:
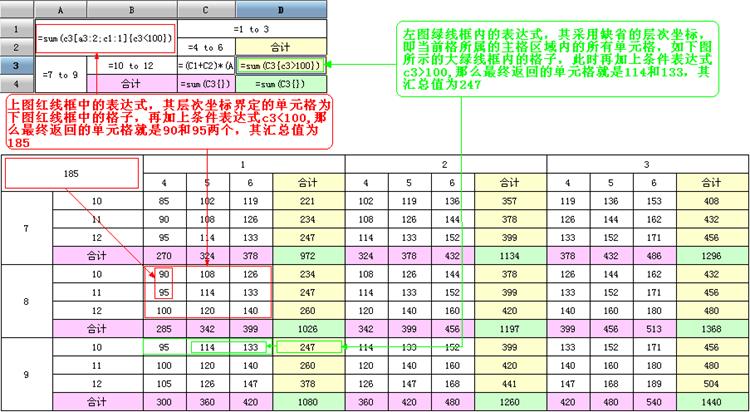
$运算符
请看下面的表格：
|
年份 |
月份 |
销售额 |
比去年同期 |
|
2005年 |
1月 |
23 |
|
|
3月 |
43 |
|
|
|
4月 |
456 |
|
|
|
7月 |
765 |
|
|
|
2006年 |
4月 |
876 |
|
|
1月 |
98 |
|
|
|
7月 |
56 |
|
该表格在设计界面中是如下样子：
|
年份 |
月份 |
销售额 |
比去年同期 |
|
A2 |
B2 |
C2 |
D2 |
可以看出，设计器中只有一行的表达式单元格，但是扩展后变成了很多的行。而该表格中的难点是计算比去年同期，也就是说，对于2006年7月份的格子来说，需要和2005年7月份的数据进行对比运算，而2006年4月份的格子需要和2005年4月份的格子进行对比运算。
而这个表格中的月份不是连续的，而且不是按顺序排列，因此仅仅靠层次坐标、位移坐标无法定位到去年同月份的单元格，需要借助条件表达式。
此时我们往d2单元格中写入表达式：C2-C2[A2:-1]{当前格的b2主格值==目标格的b2主格值}
这时我们会发现，条件表达式没法写了，当前格的主格是b2，目标格的主格也是b2，如果我们写成b2=b2，显然搞不清谁是谁的，于是我们引入了$运算符，他在格集条件表达式中指代当前格的主格
例如上面的条件表达式我们可以写成：C2-C2[A2:-1]{$B2==B2}，其中$B2指代当前格的B2主格，B2指代目标格的B2主格
总结：$运算符的书写规则如下：
$cellx
其含义是在格集表达式中指代当前格的cellx主格
定位和拉伸
报表区域
例1：
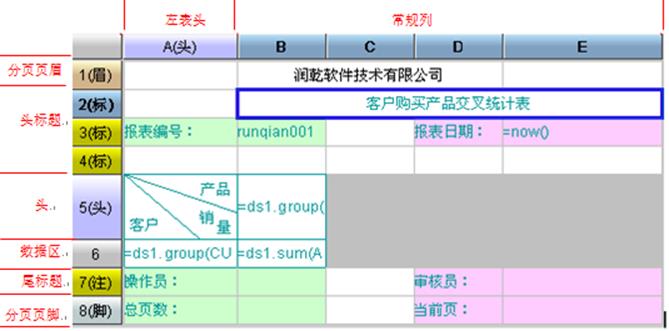
1、 横向分区从左到右的顺序为：左表头à常规列à右表头
2、 纵向分区从上到下的顺序为：分页页眉à头标题à报表头à分组表头à数据区à表尾区à尾标题à分页页脚。
3、 区域顺序从左到右、从上到下不可颠倒
4、 除了数据区，其它区域可以不存在
5、 合并格不能跨越区域，否则分页时会出现混乱
6、 除报表头、分组表头、数据区和表尾区以外的区域适用定位和拉伸规则
空白单元格优先占用
报表设计的时候，由于数据区单元格是横向扩展的，因此经常出现数据区只需要两三列的单元格，而标题区由于不是扩展的，往往需要报表编号、日期、制表人等等信息，导致标题区需要四五列甚至更多的单元格，而报表的展现模型又是严格的矩形，由此导致数据区会出现一些没用的单元格，为了避免这些没用的单元格占用内存，可以把这些单元格设为空白单元格。
所谓空白单元格，就是不存储任何属性的单元格，他仅仅起个占位的作用，保证报表始终是个完整的矩形，因此在内存中他基本不占用内存。
例1:
规则：
当数据区向右、下进行扩展复制时，如果紧邻的右、下方有空白单元格，那么空白单元格的位置会被优先占用，之后才会继续向右、下复制。
分页时伸缩规则
数据区横向扩展时，很可能横向扩展出很大面积，但是头标题区和尾标题区在设计的时候无法知道数据区会扩展出多大，而为了让报表整体美观，报表的标题区和尾标题区都是希望随着数据区的横向扩展，头标题区和尾标题区有些内容要靠右对齐，有些内容要靠左对齐。这时，我们建议除了希望靠左靠右对齐的单元格外，对中间某一单元格设置“分页时伸缩“属性，这样，横向扩展时报表引擎会对该单元格进行拉大。这就是分页时伸缩规则。
报表头、分组表头、数据区、表尾区横向扩展时，其它区域的单元格从右往左数，找到第一个设置“分页时伸缩”属性的单元格，对其进行拉伸。如果没有单元格设定了分页时伸缩，则对最右边一个单元格进行拉伸。
例1:
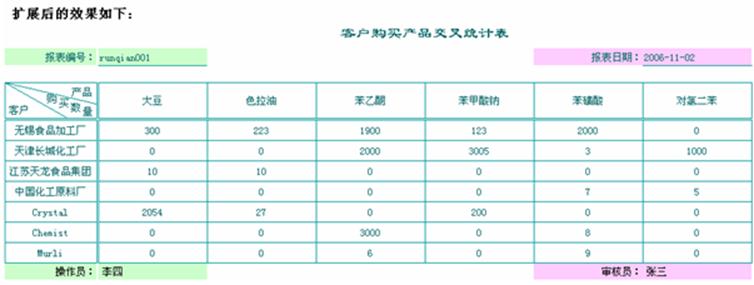
位置不变
报表头、报表尾、分组头、数据区单元格进行横向扩展时，其它区域的单元格有可能要靠左对齐，因此除了分页时伸缩规则，我们还定义如下规则：
报表头、报表尾、分组表头、数据区单元格进行横向扩展时，其它区域的单元格除了向右靠齐和被拉大的单元格，其余单元格保持位置不变。