线性代数函数
集算器中可以直接使用一些有关矩阵运算的函数,如矩阵相乘,计算矩阵的行列式等。而用来计算以及结果中得到的矩阵用二维序列来表示。
向量和矩阵
在集算器中,可以用序列和二维序列来表示向量和矩阵:
|
|
A |
|
1 |
[-5, 8, 11] |
|
2 |
=A1(3) |
|
3 |
[[-5, 8, 11]] |
|
4 |
[[1,3,5],[2,4,7]] |
|
5 |
=A4(2)(1) |
|
6 |
=transpose(A4) |
A1中用序列直接定义向量,这种向量和显示结果相同,是单列的纵向量:
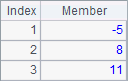
在列向量中,可以和序列一样按序号获取其中某行的数值,如A2所示:
![]()
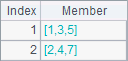
向量分为单列的纵向量和单行的横向量,在一些线性代数函数中可以根据需要自动转换。如果需要直接定义单行的横向量,可以使用A3中的方式,相当于定义单行的矩阵:
![]()
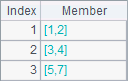
定义一般的矩阵时,和使用二维序列是相同的,序列中的每一个成员都是一个矩阵中的一行。从矩阵中可以根据行列号获取其中的某个成员,如A5中获取矩阵中的第2行第1列的数值。A4和A5中的结果如下:
![]()
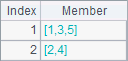
使用transpose() 函数,可以将矩阵的行列转置,即行变为列,列变为行。如A6中将2*3的矩阵转置为3*2矩阵,结果如下:
|
|
A |
|
1 |
[[1,3,5],[2,4]] |
|
2 |
=A1(2) |
|
3 |
=A1.(~(2)) |
|
4 |
=A1.len() |
|
5 |
=A1.max(~.len()) |
从矩阵中获取某一行,可以直接按行号获取,但是获取某一列时则需要使用序列的循环计算,如A1中的初始序列,以及A2和A3中获取的第2行和第 2列的结果如下:
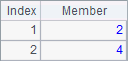
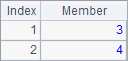
如果矩阵中存在空位置,在获取某列时有可能会出现错误,因此建议定义矩阵时,即使是空值也需定义,如将A1中的定义改为:[[1,3,5],[2,4,]]。
矩阵的长度称为矩阵的行数,可以用A.len() 函数直接获取,矩阵中各行的长度称为矩阵的列数,在矩阵未定义满时需要用A5中的方式计算,获取各行的最大列数。计算后,A4和A5中的结果如下:
![]()
![]()
为了避免上面这样的问题,定义矩阵时各行的列数应该相同。
基本计算
行列数相同的向量或矩阵,可以对位做四则运算,此时使用序列的对位计算来执行,如:
|
|
A |
B |
|
1 |
[1,1,0,0] |
[1,2,3,4] |
|
2 |
[[1,3,5],[2,4,7]] |
[[-5, 8, 11], [3, 9, 21]] |
|
3 |
=A1++B1 |
=A1--B1 |
|
4 |
=A2.(~++B2(#)) |
=A2.(~--B2(#)) |
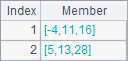
A3和B3计算两个向量对位成员相加或相减的结果如下:
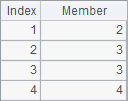
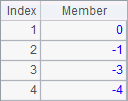
A4和B4中计算两个矩阵对位成员相加或相减的结果如下:

在线性代数基本计算中,更常见的是计算两个向量或者矩阵相乘的结果,如:
|
|
A |
B |
|
1 |
[1,1,0] |
[1,2,3] |
|
2 |
=mul(A1,B1) |
=mul([A1],B1) |
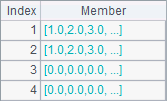
A2中用mul() 函数计算两个向量的乘积,默认情况下会计算两个向量的外积,同时计算时会采用双精度计算以保证精度。A2中计算两个3行向量的外积,会自动将第2个纵向量转置为横向量,得到的外积为3*3矩阵,如下:
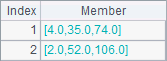
如果需要计算两个向量的内积,那么第一个向量需为横向量,B2中得到的结果为标量,如下:
![]()
计算矩阵相乘时,同样使用mul() 函数,如:
|
|
A |
B |
|
1 |
[[1,3,5],[2,4,7]] |
[[-5, 8, 11], [3, 9, 21], [4, , 8] |
|
2 |
[8, 9, 0] |
|
|
3 |
=mul(A1,B1) |
=mul([A1(2)], B1.(~(2))) |
|
4 |
=mul(A1, A2) |
|
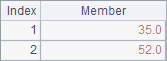
矩阵在计算相乘的结果时,第一个矩阵的列数必须与第2个矩阵的行数相等,否则无法计算。A3中计算A1和B1中两个矩阵相乘的结果如下:
在mul(A, B) 的结果中,结果中第m行n列的每个成员都是A矩阵中第m行与B矩阵中第n列的内积,如B3中计算第2行第2列的结果如下:
![]()
还可以用mul() 函数计算矩阵与向量相乘,如A4中结果如下:
除了计算矩阵相乘,在集算器中还提供了计算矩阵行列式、秩以及矩阵求逆等函数:
|
|
A |
B |
|
1 |
[[1, 0, 2], [-1, 5, 0], [0, 3, -9]] |
[[3, 2, 4], [-1, 1, 2], [9, 5, 10]] |
|
2 |
=det(A1) |
=det(B1) |
|
3 |
=rankm(A1) |
=rankm(B1) |
|
4 |
=inverse(A1) |
|
用det() 函数可以计算矩阵行列式的值,如果矩阵不满秩,得到的结果会是0,A2和B2中结果如下:
![]()
![]()
用rankm() 函数可以计算矩阵的秩,A3和B3中得到两个矩阵的秩如下:
![]()
![]()
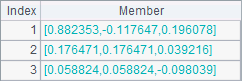
行数和列数相等的矩阵称为方阵,用inverse() 函数可以计算n阶方阵的逆矩阵,计算时要求矩阵必须可逆,即矩阵的秩为n或者矩阵的行列式不为0。A4中得到A1的逆矩阵如下:
数学计算
除了向量和矩阵的基本计算,集算器还提供了一些矩阵和向量的数学计算函数,如计算方差、标准差等:
|
|
A |
B |
|
1 |
[4, 1, 10] |
[-7, 4, 7] |
|
2 |
=var(A1) |
=var@s(A1) |
|
3 |
=mse(A1, B1) |
=mae(A1, B1) |
|
4 |
=dis(A1, B1) |
|
|
5 |
=dis@a(A1, B1) |
=dis@m(A1, B1) |
用var() 函数可以计算向量的总体方差,如果添加@s选项则计算的是统计时常用的样本方差,A2和B2中结果如下:
![]()
![]()
用mse()和mae() 函数可以计算两个向量的标准误差和绝对误差,A3和B3中结果如下:
![]()
![]()
用dis() 函数可以计算两个向量间的欧氏距离,添加@a选项计算距离时将计算绝对值的和,添加@m选项将根据向量长度求均值。A4, A5和B5中结果如下:
![]()
![]()
![]()
用pearson() 函数和spearman()函数,可以计算两个向量的皮尔逊相关系数和斯皮尔曼相关系数:
|
|
A |
B |
|
1 |
[4, 1, 10] |
[-7, 4, 7] |
|
2 |
=pearson(A1, B1) |
=spearman(A1, B1) |
|
3 |
=pearson@r(A1, B1) |
=pearson@a(A1, B1; 2) |
A2和A3中得到的pearson相关系数和spearman相关系数如下:
![]()
![]()
使用pearson() 函数时,可以添加@r选项在计算前先对向量做均值化处理,添加@a选项可以设置计算时的自由度,A3和B3中的结果如下:
![]()
![]()
还有一些函数可以用来对向量或者矩阵执行数据处理,如:
|
|
A |
B |
|
1 |
[4, 1, 10] |
[[8, 1, 6], [3, 5, 7], [4, 9, 2]] |
|
2 |
=norm(A1) |
=norm@0(A1) |
|
3 |
=norm@s(A1) |
=norm(B1) |
使用norm()函数可以对向量做归一化处理,添加@0选项时,只线性调整使得向量的均值为0,添加@s选项时,将调整向量使得向量的均值为0同时标准差为1。计算后,A2,B2和C2中结果如下:
![]()
![]()
![]()
还可以使用矩阵作为参数,分别对每一行执行归一化处理。B3中结果如下:

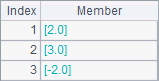
用linefit(A, Y) 函数可以用最小二乘法做线性拟合,其中A为系数矩阵,Y为常数矩阵,两者行数相同。当A为n阶方阵,Y为向量时相当于求解矩阵方程AX=Y,如:
|
|
A |
B |
|
1 |
[[1,-2, 3],[2,3,4],[3,5,7]] |
[-10,5,7] |
|
2 |
=linefit(A1,B1) |
|
计算后A2中结果如下:
使用polyfit(A, B, n)函数可以用n次多项式拟合两个向量,返回的结果为从低到高的系数序列,如:
|
|
A |
B |
|
1 |
[1,2,3,5] |
[2,13,38,155] |
|
2 |
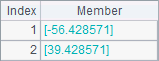
=polyfit(A1,B1,1) |
=polyfit(A1,B1,2) |
|
3 |
=polyfit(A1,B1,3) |
|
A2,B2和A3中分别使用了不同的次数来拟合两个同样的向量,计算后的结果分别如下:
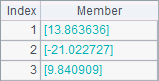
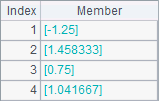
如A3中的拟合结果即为1.041667x3+0.75x2+1.458333x-1.25。
