八皇后
l 思路
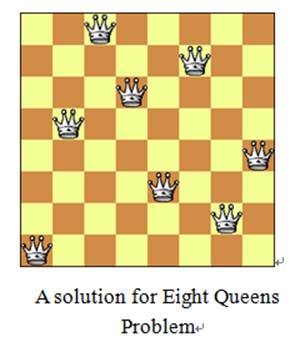
八皇后问题是一个古老而著名的问题。具体为:在8X8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,请问有多少种摆法。
l 思路
先将8X8格的国际象棋上的每一行作为一个序列,将列上的每一个格子按顺序编号1,2,3,4,5,6,7,8
1. 初始时将第一个皇后放在第一行第一列上,并在序列中进行标记
2. 转入下一行进行判断,如果该行该列上已经存在一个皇后,则在该行上将皇后后移一列,如果已经移到了最后一列,则回溯到上一行,将上一行的皇后的位置后移一列
3. 判断所在行的皇后是否与以上的所有行是否在同一斜线上,如果在同一斜线上,则将所在行皇后向后移一列,如果如果已经移到了最后一列,则回溯到上一行,将上一行的皇后的位置后移一列
l 代码
|
|
A |
B |
C |
D |
|
|
1 |
=[0]*8 |
>i=1 |
|
|
A1存储棋盘的每行的皇后所在的位置,B1初始起始行 |
|
2 |
for i>0 |
>A1(i)=A1(i)+1 |
|
|
B2设置第i行皇后的位置,从1开始逐位判断是否合理 |
|
3 |
|
if A1(i)==9 |
>A1(i)=0,i=i-1 |
next |
如果当前行皇后的位置设置到了最后一列仍旧不合理,则将该行的皇后先移除,回溯到上一行,调整上一行的皇后位置 |
|
4 |
|
if i==1 |
>i=2 |
next |
第一行不用判断,直接进行下一行的判断 |
|
5 |
|
=A1(i) |
=A1(to(i-1)) |
|
|
|
6 |
|
if C5.pos(B5)>0 |
next |
|
如果当前行皇后所在的列已经存在了皇后,将当前行皇后的位置后移一列,重新判断 |
|
7 |
|
if C5.pselect(i-# ==abs(B5-~))>0 |
next |
|
如果当前行皇后所在的斜线已经存在了皇后,将当前行皇后的位置后移一列,重新判断 |
|
8 |
|
>i=i+1 |
|
|
如果该行皇后满足条件,跳转到下一行 |
|
9 |
|
if i==9 |
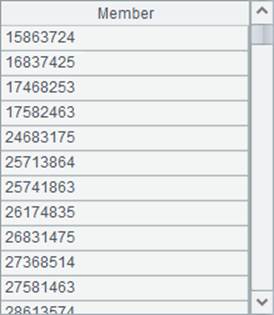
=C9|A1.concat() |
>i=i-1 |
如果8行全部设置完毕,将结果存储,通过修改上一行的结果再次进入到循环,查找下一种摆放方式 |
|
10 |
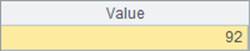
=C9.len() |
|
|
|
算出所有摆法的数量 |
l 结果